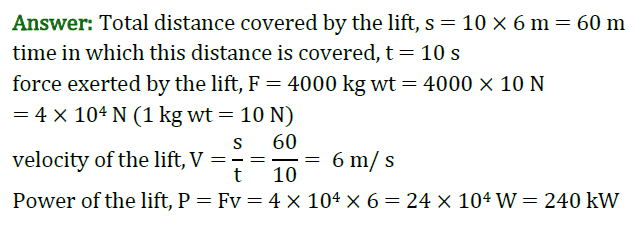Extra Questions for Class 9 Science Chapter 11 Work and Energy
Extra questions for Class 9 Science Chapter 11 Work and Energy with answers is given below. Our subject expert prepared these solutions as per the latest NCERT textbook. These questions will be helpful to revise the all topics and concepts. CBSE Class 9 extra questions are the most simple and conceptual questions that are prepared by subject experts for the students to study well for the final exams. By solving these extra questions, students can be very efficient in their exam preparations.
Work and Energy Class 9 Science Extra Questions and Answers
Very Short Answer Questions
1: What is the work done against the gravity when a body is moved horizontally along a frictionless surface?
Answer: Zero
2: When displacement is in a direction opposite to the direction of force applied, what is the type of work done?
Answer: Negative work.
3: A 40 kg girl is running along a circular path of radius 1 m with a uniform speed. How much work is done by the girl in completing one circle?
Answer: Zero
4: Seema tried to push a heavy rock of 100 kg for 200 s but could not move it. Find the work done by Seema at the end of 200 s.
Answer: Work done = 0 Since displacement, s = 0
5: Identify the kind of energy possessed by a running athlete.
Answer: Kinetic energy.
Short Answer Type Questions
1: An electrical heater is rated 1200 W. How much energy does it use in 10 hours?
Answer: Electrical energy = Power × time taken
= 1.2 × 10
= 12 kWh
2: If an electric appliance is rated 1000 W and is used for 2 hours. Calculate the work done in 2 hours.
Answer: Work done = Energy consumed
Energy = Power × Time taken
= 1000 W × 2 hour
= 2000 W-hr or 2 kW-hour or 2 kWh
3: A man of mass 62 kg sums up a stair case of 65 steps in 12 s. If height of each step is 20 cm, find his power.
Answer: m = 62 kg, g = 10 m/s2
h = 65 × 20/100 = 13 m
P.E. = mgh
P.E. = 62 × 10 × 13
= 8060 J
Power (𝑃) = (𝑃.𝐸.)/𝑡
= 8060/12
= 671.67 𝑊
4: How is work done by a force measured? A porter lifts a luggage of 20 kg from the ground and puts it on his head 1.7 m above the ground. Find the work done by the porter on the luggage. (g = 10m/s2)
Answer: Work done is product of force and displacement
W=F × s
m=20 kg
g=10m/s2
h =1.7𝑚
The work done by the porter = mgh
= 20 × 10 × 1.7
= 340 J
5: The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
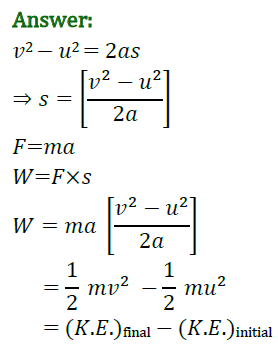
6: When a force retards the motion of a body, what is the nature of work done by the force? State reason. List two examples of such a situation.
Answer: The work done by the force is negative because the displacement is opposite to the direction of force applied.
Example: (i) Work done by the force of friction;
(ii) Work done by applying brakes.
7: When is the work done by a force said to be negative ? Give one situation in which one of the forces acting on the object is doing positive work and the other is doing negative work.
Answer: Negative work: When the force is acting opposite to the direction of the displacement, the work done by the force is said to be negative. When we lift an object, two forces act on the
(i) Muscular force: Doing positive work in the direction of the displacement.
(ii) Gravitational force: Doing negative work opposite to the direction of the displacement.
8: (a) Under what conditions work is said to be done?
(b) A porter lifts a luggage of 1.5 kg from the ground and puts it on his head 1.5 m above the ground. Calculate the work done by him on the luggage.
Answer:(a) (i) Force should be applied.
(ii) Body should move in the line of action of force.
(iii) Angle between force and displacement should not be 90°.
(b) Mass of luggage, m = 15 kg and displacement, s = 1.5 m.
Work done, W = F×s = mg × s = 15 × 10 × 1.5 = 225 J
9: Four persons jointly lift a 250 kg box to a height of 1 m and hold it.
(i) Calculate the work done by the persons in lifting the box.
(ii) How much work is done for just holding the box ?
(iii) Why do they get tired while holding it ? (g = 10ms2)
Answer: (i) F = 250 × 10 = 2500𝑁
s =1 m
W = F ×s
= 2500 ×1|
=2500𝐽
(ii) Zero, as there is no displacement.
(iii) To hold the box, men are applying a force which is opposite and equal to the gravitational force acting on the box. While applying the force muscular effort is involved, and so they feel tired.
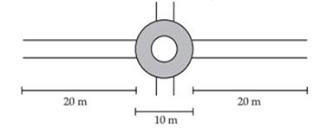
10: A boy is pulling a cart by supplying a constant force of 8 N on a straight path of 20 m. On a round about of 10 m diameter he forgets the path and takes 1½ turns and then continues on the straight path for another 20 m. Find the net work done by the boy on the cart.
Answer: F = 8N
Work done, W = F × s
W1 = 8 × 20
= 160 J
D =10 m
So radius,
D/2 = 10/2 = 5m
Circumference of a circle = 2πr
= 2 × 22/7 × 5
= 31.43
Distance in 1⁄2 circle = πr
= 22/7 × 5
= 15.71
Total distance for 1 ½ circle = 31.43 + 15.71 = 47.14 m
W2 = F × s
= 8 × 47.14
= 376 J
W3 = 20 × 8 = 160 J
Total work done = 160 + 376 + 160
= 696 J
Long Answer Type Questions
1: Calculate the electricity bill amount for a month of 30 days, if the following devices are used as specified:
(i) 2 bulbs of 40 W for 6 hours.
(ii) 2 tubelights of 50 W for 8 hours.
(iii) A TV of 120 W for 6 hours.
Given the cost of electricity is ₹2.50 per unit.
Answer: Given the cost of electricity is ₹2.50 per unit.
(i) 2 bulbs of 40 watts for 6 hrs.
Energy consumed by Bulbs E1 = 2 × 40 × 6 = 480 W = 0.48 kWh
(ii) Energy consumed by 2 tubelights E2 = 50 × 8 × 2 = 0.800 kWh
(iii) Energy consumed by TV E3 = 120 × 6 = 0.720 kWh
Total Energy = 0.48 + 0.80 + 0.72
= 2.00 units rate
= 2.50 per unit
Cost per day = 2 × 2.50 = 5.00
Cost 30 days = 5.00 × 30 = 150
2: (i) What is meant by mechanical energy? State its two forms. State the law of conservation of energy. Give an example in which we observe a continuous change of one form of energy into another and vice-versa.
(ii) Calculate the amount of work required to stop a car of 1000 kg moving with a speed of 72 km/h.
Answer: (i) Sum of kinetic energy and potential energy of an object is the total mechanical energy.
Its two forms are kinetic energy and potential energy.
Energy can neither be created nor be destroyed but can be transformed from one form to another. One example is simple pendulum.
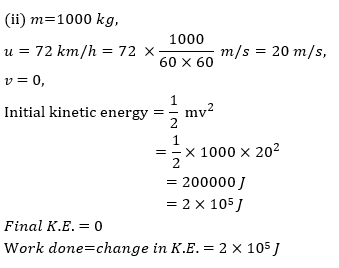
3. A boy pushes a book by applying a force of 40N. Find the work done by this force as the book is displaced through 25 cm along the path.
Answer: Here, force acting on the book, F = 40N
distance through which book is displaced, s = 25 cm = 0·25 m
Work done by the force, i.e., W = F × s
= (40 N) (0·25 m)
= 10J
4. A ball of mass 1 kg thrown upwards, reaches a maximum height of 4 m. Calculate the work done by the force of gravity during the vertical displacement. (g = 10 m/s2).
Answer: Here, force of gravity on the ball, F = mg = (1 kg) (10 m/s2) = 10N
vertical displacement of the ball, s = 4m
Since the force and the displacement of the ball are in opposite directions, work done by the force of gravity, i.e., W= F × s
= 10 × 4
= 40J
Obviously, work done against the force of gravity = 40J
5. An engine pulls a train 1 km over a level track. Calculate the work done by the train given that the frictional resistance is 5 × 105 N.
Answer: Here, frictional resistance, F = 5 × 105 N
distance through which the train moves, s = 1 km = 1000 m
Work done by the frictional force, i.e.,
W = Fs = (5 × 105) × 1000 = 5 × 108 J
(F and s are in opposite directions)
Obviously, work done by the train is 5 × 108 J
6. A man weighing 70 kg carries a weight of 10 kg on the top of a tower 100 m high. Calculate the work done by the man. (g = 10 m/s2).
Answer: Here, force exerted by the man,
F = (70 + 10) = 80 kg wt
= 80 × 10
= 800 N
vertical displacement, s = 100 m
Work done by the man, i.e.,
W = F × s
= (800N) (100m)
= 80000 J
7. How fast should a man of mass 60 kg run so that his kinetic energy is 750 J ?
Answer: Here, mass of the man, m = 60 kg
kinetic energy of the man, Ek = 750J
If v is the velocity of the man, then
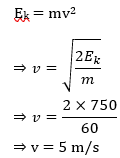
8. Find the mass of the body which has 5J of kinetic energy while moving at a speed of 2 m/s.
Answer: Here, kinetic energy of the body, Ek = 5J
speed of the body, v = 2 m/s
If m is the mass of the body, then
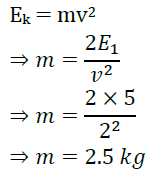
9. A player kicks a ball of mass 250 g at the centre of a field. The ball leaves his foot with a speed of 10 m/s, Find the work done by the player on the ball.
Answer: The ball, which is initially at rest, gains kinetic energy due to work done on it by the player.
Thus, the work done by the player on the ball, W = kinetic energy (Ek) of the ball as it leaves his foot, i.e., W = Ek = mv2
Here, m = 250 g = 0·25 kg,
v = 10 m/s
W = (0·25) ×(10)2
= 12·5 J
10. A body of mass 5 kg, initially at rest, is subjected to a force of 20N. What is the kinetic energy acquired by the body at the end of 10s?
Answer: Here, mass of the body, m = 5 kg
initial velocity of the body, u = 0
force acting on the body, F = 20 N
time for which the force acts, t = 10 s
If a is the acceleration produced in the body,
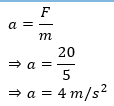
Let v be the velocity of the body after 10 s.
Clearly, v = u
We know that
V = u + at
When u = 0
v = 0 + at
⇒ v = 4 × 10
⇒ v = 40 m/s
Kinetic energy acquired by the body,
Ek = mv2
= 5 × (40)2
= 4000J
11. A bullet of mass 20 g moving with a velocity of 500 m/s, strikes a tree and goes out from the other side with a velocity of 400 m/s. Calculate the work done by the bullet in joule in passing through the tree.
Answer: Here, mass of the bullet, m = 20 g = 0·02 kg
initial velocity of the bullet, u = 500 m/s
final velocity of the bullet, v = 400 m/s
If W is the work done by the bullet in passing through the tree, then according to work-energy theorem
W = mu2 – mv2
= m(u2 – v2)
= (0·02) [(500)2 – (400)2]
= 900J
12. A body of mass 4 kg is taken from a height of 5 m to a height 10 m. Find the increase in potential energy.
Answer: Here, mass of the body, m = 4 kg
increase in height of the body, h = (10 – 5) = 5m
Increase in potential energy,
Ep = mgh
= 4 × 10 × 5
= 200J
Initial potential energy of the body,
Epi = mgh
= 4 × 10 × 5
= 200J
Final potential energy of the body,
Epf = mghf
= 4 × 10 × 10
= 400J
Increase in potential energy,
Ep = Epf – Epi
= 400J – 200J
= 200J
13. A 5 kg ball is thrown upwards with a speed of 10 m/s.
(a) Find the potential energy when it reaches the highest point.
(b) Calculate the maximum height attained by it.
Answer: (a) Here, mass of the ball, m = 5 kg,
speed of the ball, v = 10 m/s
Kinetic energy of the ball,
Ek = mv2
= 5 × (10)2
= 250J
When the ball reaches the highest point, Its kinetic energy becomes zero as the entire kinetic energy is converted into its potential energy (Ep) i.e., Ep = 250J ….(i)
(b) If h is the maximum height attained by the ball,
Ep = mgh …. (i)
From eqn. (i) and (ii),
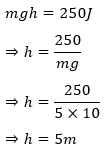
14. A 5 kg ball is dropped from a height of 10m.
(a) Find the initial potential energy of the ball.
(b) Find the kinetic energy just before it reaches the ground and
(c) Calculate the velocity before it reaches the ground.
Answer: Here, mass of the ball, m = 5 kg
Height of the ball, h = 10m
(a) Initial potential energy of the ball,
Ep = mgh = 5 × 10 × 10 = 500J
(b) When the ball reaches the ground, its potential energy becomes zero as it is entirely converted into its kinetic energy (Ek), i.e., Ek = 500J
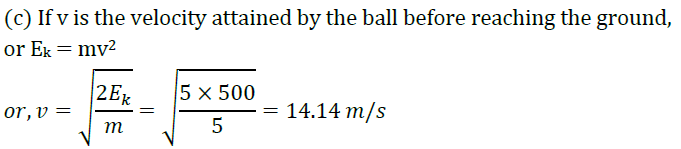
15. A body is thrown up with a kinetic energy of 10 J. If it attains a maximum height of 5 m, find the mass of the body.
Answer: Here, kinetic energy of the body, Ek = 10J
maximum height attained by the body, h = 5m
When the body attains maximum height, its entire kinetic energy is converted into its potential energy (Ep)
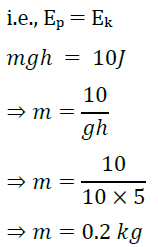
16. A rocket of mass 3 × 106 kg takes off from a launching pad and acquires a vertical velocity of 1 km/s and an altitude of 25 km. Calculate its (a) potential energy (b) kinetic energy.
Answer: Here, mass of the rocket, m = 3 × 106 kg
velocity acquired by the rocket, v = 1 km/s = 1000 m/s
height attained by the rocket, h = 25 km = 25000 m
(a) Potential energy of the rocket,
Ep = mgh
= (3 × 106) × (102) × 25000
= 7.5 × 1011 J
(b) Kinetic energy of the rocket,
Ek = mv2
= (3 × 106) × (1000)2
= 1.5 × 1012 J
17. A boy of mass 40 kg runs up a flight of 50 steps, each of 10 cm high, in 5 s. Find the power developed by the boy.
Answer: Here, mass of the boy, m = 40 kg
total height gained, h = 50 × 10 cm = 500 cm = 5m
time taken to climb, t = 5s
Work done by the boy,
W = mgh
= 40 × 10 × 5
= 2000J
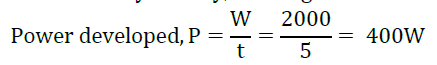
18. What should be the power of an engine required to lift 90 metric tonnes of coal per hour from a mine whose depth is 200 m
Answer: Here, mass of the coal to be lifted,
m = 90 metric tonnes
= 90 × 1000 kg
= 9 × 104 kg
height through which the coal is to be lifted, h = 200m
time during which the coal is to be lifted,
t = 1h
= 60 × 60
= 3600 s
work done to lift the coal, i.e.,
W = mgh
= 9 × 104 × 10 × 200m
= 18 × 107 J
Power of the engine required i.e.,
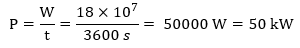
19. How much time does it take to perform 500J of work at a rate of 10W ?
Answer: Here, work to be performed, W = 500J
rate at which work is to be performed, i.e., power, P = 10W
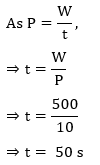
20. Calculate the units of energy consumed by 100 W electric bulb in 5 hours.
Answer: Here, power of the electric bulb, P = 100 W = 0·1 kW
time for which bulb is used, t = 5h
As P = W/t,
⇒ W = Pt
Energy consumed by the bulb,
W = Pt
= 0·1 × 5
= 0·5 kWh
= 0·5 units
21. A lift is designed to carry a load of 4000 kg through 10 floors of a building, averaging 6 m per floor, in 10 s. Calculate the power of the lift.